COVID-19が世界中で拡大しています。今後どれだけ拡大するのか、どうすれば拡大を防げるのか、専門家たちが予測しています。
予測はどのように行うのでしょうか?
指数関数的増加
その前に、感染が爆発するとどうなるのかを見てみましょう。感染者が「指数関数的に増加する」と言われることがありますが、これはどんな意味でしょうか。
Tom Rocks MathsのYouTube登録者数は8520人です。Tomはオックスフォード大学のセントエドモンドホールとセントヒューズカレッジで教鞭を執っています。流体力学や特殊関数についての動画を投稿しています。
こちらの動画で指数関数的増加についてわかりやすく説明しています。
現在、COVID-19の患者は1人あたり3人に感染を起こすと言われています1。これを「基本再生産数が3」であると言い、R0 = 3と書きます。1人の患者が5日で3人にうつし、自分は治るとしましょう。
すると、5日で3人にうつります。その後の5日(最初から数えて10日)でその3人がそれぞれ3人にうつすので9人にうつります。その次の5日(最初から数えて15日)で9人が3人にうつすので27人にうつります。その次の5日で81人、その次の5日で243人です2。
これが指数関数的増加です。動画ではTomがどんどん増殖していくので気持ち悪くてわかりやすいです。
200人を超えると、高齢者などのCOVID-19が重篤になりやすい人も一定数含まれるようになり、死亡者も出始めます。イギリスの人口構成で、30日間で17人の死者が出ると試算しています。
もし、人と人の接触を半減させることができれば状況は改善します。1人が1.5人にうつすだけなら、30日間で19人にしか感染せず、死者はほぼ0になります。これが現在、世界各地で外出制限が行われている理由です。
ちなみに、指数関数的に増加する感染者数を表示するのに有効なのが片対数プロットです。
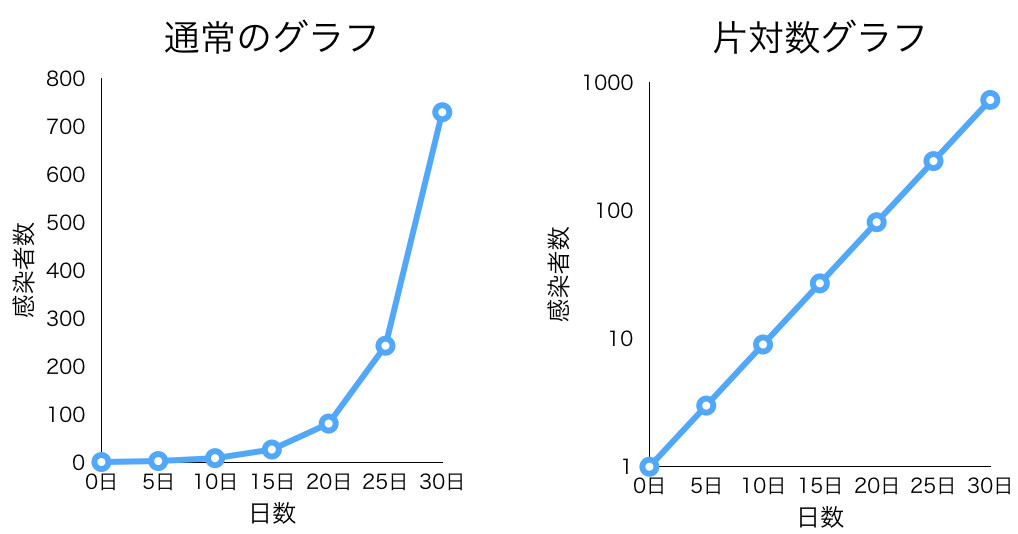
通常のグラフと片対数グラフ
左のように普通の軸で表示すると、爆発的に増加しているのはわかりますが、はじめの方がつぶれてしまって読み取りにくくなります。ところが、右のように軸を取り直すと、直線的に増える形になり、見やすくなります。これを片対数プロットと言います。片対数プロットでは指数関数的な増加は直線になります。感染症は指数関数的に増加するので、片対数プロットで表示されます。片対数プロットで直線的になっているということは、爆発的に感染者が増加しているということです。
SIRモデル入門
Trefor BazettのYouTube登録者数は3.69万人です。Treforはカナダのヴィクトリア大学の教育助教(assistant teaching professor)です。トロント大学で代数的位相幾何学の博士号をとりました。特に離散数学・線形代数・解析学の動画を投稿しています。
こちらの動画では感染症の拡大を予測するのに使われるSIRモデルを解説しています3。
SIRモデルのSとIとRはsusceptibles(感受性保持者または未感染者)、infected(感染者)、recovered(免疫保持者または回復者)の頭文字です4。SIRモデルは人々をこの3つのグループに分け、その人数がどのように推移するかを予測する数式です。現実を予測するための数式をモデルと呼びます。
S(未感染者)がI(感染者)と接触するとIになり、Iはいずれ回復してR(回復者)になります。時刻tのそれぞれの人数をS(t)、I(t)、R(t)と表します。
総人口をNと表します。最初の時刻、t = 0ではほとんど全員が未感染で、ごく一部だけが感染者です。これはCOVID-19の感染拡大初期にあたります。この後、未感染者が減り、感染者が増え、回復者も遅れて増えてきますが、総人口は変わりません。つまり、
![]()
がどのtでも成り立ちます。
感染者の人数はどのように変化していくでしょうか? つまり、I(t)はtが変化するとどのように変化していくでしょうか? これは、SやIやRの変化速度を求めればわかります。
ある量の時間が経ったときの変化の測度を表すのが、時間についての微分です。つまり、
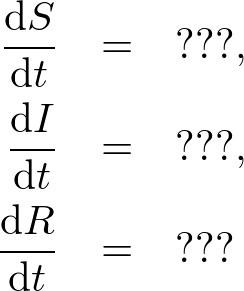
の???のところがわかればよいことになります。
まず、未感染者S(t)がどのように変化するかから考えましょう。Sが多ければ多いほど新たに感染する人が多くなります。つまり、Sが大きいと減少速度が大きくなります。しかし、Sが多くても感染者Iがいなければ感染が起こりません。新たな感染者が発生してSが減るのはSとIが出会ったときです。出会う回数は人数に比例しますから、
![]()
となります。aは正の数です。未感染者と感染者が接触したときにどれぐらい感染が起こりやすいかを表します。
それでは、感染者I(t)はどのように変化するでしょうか。まず、Sが減った分だけ増えます。
![]()
そして、一定の率で回復していきます。感染者が多ければ多いほど、回復する人は増えます。回復する人の人数は感染者に比例するでしょう。つまり、
![]()
となります。bも正の数です。回復者は感染者のうち回復した分だけが増えるので、
![]()
となります5。
これがSIRモデルです。
SIRモデルを使って感染が拡大するかしないかを調べてみましょう。初期の感染者の増加の速度は
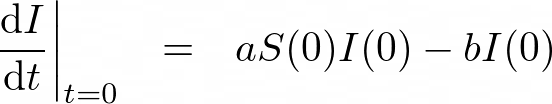
となります。これが正の値なら感染は拡大し、負の値なら感染は収束します。ということは、右辺を変形して、
![]()
のときに感染は拡大します。このaS(0)/bが基本再生産数R0です。基本再生産数が1より大きければ感染は拡大し、1より小さければ収束します。
どうすれば基本再生産数は小さくなるのでしょうか。aは未感染者と感染者の接触でどれぐらい感染が起こりやすいかを表すものです。手洗いなどで感染が起こりにくくなれば基本再生産数は小さくなります。ワクチンを使って感染しうる人S(0)を減らすのも有用です6。
感染が拡大する場合、感染は初期にどのように広がるでしょうか。初期にはS(t)が非常に大きく、ほとんど変化しないとすると、元の微分方程式は
![]()
に近いものになります。この微分方程式は解くことができ、指数関数で表せることがわかります。つまり、指数関数的増加がSIRモデルから出てくるのです。こちらのページで見られる“Total Cases excluding mainland China”を片対数プロットで見ると7直線的になっているのを示しています。
感染症の拡大はこのようなモデルで予測されます8。数学の威力がわかる動画でした。


